A thin wire, moving through the air, is made to vibrate in the audio range at the vortex shedding frequency.
What it Shows
When air flows around an object, there is a range of flow velocities for which a von Karman vortex street is formed. The shedding of these vortices imparts a periodic force on the object. The force is quite small and not enough to accelerate the object to any significant amount, especially if the object is relatively massive. If the situation is such that the object can vibrate about a fixed position, we have the possibility of simple harmonic motion; and if the frequency of the periodic driving force matches the natural frequency of the oscillation, then resonance obtains.
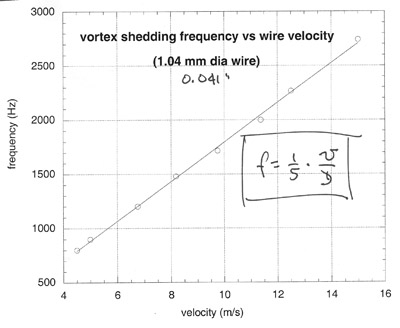
The objects are two #18 [0.041" (1.04 mm) diameter] 82.5 cm long music wires rotating through the air in a 80 cm diameter circle. The rate of rotation is continuously adjustable, providing linear velocities from "very slow" up to about 15 m/s. The wires are put under tension so that their fundamental frequency of vibration is about 120 Hz. When the vortex shedding frequency matches one of the higher harmonics of the wires, the amplitude of that mode of oscillation builds up to the point where one actually hears it "sing." It starts to sing at a velocity around 4.75 m/s at 845 Hz, the 7th harmonic. One can readily secure higher harmonics up to the 22nd at 2.7 kHz. You can hear these in the video:
Check out our demo in action: https://youtu.be/-zHh2VSHhhA
The following graph shows eight audible frequencies as a function of wire velocity. The frequencies were determined with a spectrum analyzer.
How it Works
Consider the flow of fluid around a smooth cylindrical object. For velocities exceeding laminar flow, the inertia of the fluid starts to become significant and, as the fluid stream passes the topmost part of the cylinder, it is unable to negotiate the rear half of the cylinder. Hence the fluid tends to separate from the top surface and peel off in a clockwise motion as it approaches the rear end of the cylinder, ending up as a shed vortex (it will peel off in a CCW motion from the bottom surface). For a given velocity of flow, this model suggests the vortex formation time will be proportional to the distance around the cylinder (or its diameter) and thus the frequency of vortex formation will be inversely proportional to the diameter. Furthermore, if the flow velocity increases, the frequency of vortex formation will likewise increase, leading to a direct relation between the two. This is what Strouhal found empirically in 1878[1].
The proportionality constant is called the Strouhal number and turns out to be a function of the Reynolds number. For that reason it is now known as the Strouhal-Reynolds number. It is very nearly equal to 0.2 for a large range of Reynolds numbers.
Strouhal's empirical formula for the frequency of vortex shedding is
\(f = {v\over 5d}\)
where v is the velocity of flow and d is the diameter of the cylinder (a full and modern treatment of vortex shedding can be found in references [2][3][4]). Thus, for air flowing past a 1 mm diameter cylinder at a velocity of 5 m/s, one would expect a frequency of 1 kHz.
Setting it Up
The entire apparatus sits on a dedicated cart as shown in the video. Use a separate cart for the speed control[7] and frequency counter (oscilloscope).
The operator and other people must stay clear of the apparatus at all times! Getting hit by the rotating rods and/or wires could result in very serious injuries.
The following table will help the demonstrator find suitable rotation speeds. The "setting" pertains to the knob on the speed control—consider it as a "coarse" adjustment. The rotation speed is monitored by a pick-up coil mounted on the frame. Two magnets attached to the large rotating pulley produce pulses in the pick-up coil as they pass over the coil. The magnitude of the pulses depends on the speed of rotation and increases to 62 Vp-p at maximum speed. You can use a frequency counter or oscilloscope (preferred, because you can see what you're triggering on) to measure the rate of rotation, keeping in mind that the actual rate is half the rate of pulses. Velocities in the table have been calculated knowing that the circumference of the circle the wire travels on is 2.5 meters.
| speed control setting | pulse frequency | vortex frequency | velocity |
|---|---|---|---|
| 34 - 35 | 3.6 - 3.8 Hz | 800 Hz | 4.5 m/s |
| 40 | 4.7 | 1 kHz | 5.8 |
| 45 - 47 | 5.4 - 5.8 | 1.26 | 6.75 |
| 52 | 6.5 - 6.6 | 1.4 | 8.19 |
| 59 - 60 | 7.7 - 8 | 1.7 - 1.8 | 9.75 |
| 66 - 68 | 9.0 - 9.4 | 2.1 | 11.4 |
| 72 - 75 | 10.0 - 10.5 | 2.3 | 12.5 |
Comments
Vortex-induced vibrations are important in that they can have a strong influence in countless situations ranging from tethered structures in the ocean, pipes bringing oil from the ocean floor to the surface, aeolian harps, tall buildings, and chimneys, to name but a few. For example, the tallest building in the world, the Burj Khalifa in Dubai, UAE, incorporates a variation in cross section with height to help ensure that vortices are not shed coherently along the entire height of the building.[5] The Tacoma Narrows Bridge collapse is discussed in practically every introductory physics course as a dramatic example of resonance. Although vortex shedding is often cited as being the culprit, Billah & Scanlan say that this is oversimplified physics and posit that the real culprit was flutter—a non-linear phenomenon in which the motion of the bridge was the source of self induced periodic impulses.[6]
As with most fluid dynamics phenomena, the physics of vortex-induced vibrations is quite rich and very complicated. For example, various vortex wake modes are possible with fluid flow jumping from one mode to another. Additionally, the motion of the object in the fluid affects the formation and/or shedding of vortices and can have a positive or negative feedback effect. Also, depending on the phase between object and fluid motion as well as their frequency difference, a lock-in or synchronization effect may or may not occur. Furthermore, the ratio of the object-to-fluid mass as well as damping forces have a significant effect, leading to parameters described in the literature as effective mass, critical mass, high-mass ratio, etc. Reference [4] is an excellent resource for those that wish to go deeper into the subject matter—and it can be quite deep indeed!
References
[1] V. Strouhal, "Ueber eine besondere Art der Tonerregung," Ann. Physik. Chem (Leipzig) 5(10), 216-251 (1878).
[2] C.H.K. Williamson, "Vortex Dynamics in the Cylinder Wake," Annual Review of Fluid Mechanics 28, 477-539 (1996).
[3] U. Fey, M. König, and H. Eckelman, "A New Strouhal-Reynolds-number relationship for the circular cylinder in the range 47<Re<2×105," Physics Fluids 10(7), 1547-1549 (1998).
[4] C.H.K. Williamson and R. Govardhan, "Vortex-Induced Vibrations," Annual Review of Fluid Mechanics 36, 413-445 (2004).
[5] P.A. Irwin, "Vortices and tall buildings: A recipe for resonance," Physics Today 63(9), 68-69 (2010).
[6] K.Y. Billah and R.H. Scanlan, "Resonance, Tacoma Narrows bridge failure, and undergraduate physics textbooks," Am. J. Phys. 59(2), 118-124 (1991).
[7] Leeson Speedmaster motor control, model 174307.00. This controls a DC Motor NEMA 56C, 90 VDC, 1/4 hp, 1750 rpm. The motor and drive shaft pulleys are 2-1/2" and 10-3/4" respectively to allow for higher motor rpm (one gains torque and better speed control).