Model to show celestial sphere; larger version has capacity to show lunar motions.
What it shows:
The position and motions of heavenly bodies are projected against a hypothetical sphere of infinite radius, centered on the Earth, called the Celestial Sphere. With this demo you can explain the motions of the stars and of the Sun, and show various aspects of the seasons.
How it works:
The main features of the sphere itself are shown schematically in figure 1. The spherical wire cage defines the celestial sphere, its pole aligning with the Earth's north pole and its equator defined as the projection of the Earth's equator onto the sphere. The Ecliptic is a ring that marks the Sun's path through the heavens; it is inclined at an angle of 23.5° to the celestial equator. A tilting plane defines the observer's horizon, which is at 90° to the observer's latitude. The spherical cage rotates, while the Earth at the center remains stationary. The whole sphere is mounted on a platform that can be tilted to put the observer's horizon plane can be aligned horizontally; this simplifies things a bit. With the sphere, several basic aspects of celestial motion can be demonstrated.
The stars, 'fixed' to the sphere, make a complete revolution with the sphere east to west, in 23hr 56min, known as a sidereal day.
The Sun moves on the sphere east to west one revolution per day, but also has a long term motion west to east along the ecliptic of 1° per day. The points at which the ecliptic cross the celestial equator are called the Vernal (March 21) and Autumnal (September 23) equinoxes. The maximum elevation of the ecliptic above the celestial equator is the Summer Solstice (June 21) when the Sun is directly overhead at a latitude of 23.5° north, the Tropic of Cancer. The maximum declination below the equator occurs on December 21, when the Sun is directly above the Tropic of Capricorn, 23.5° south. The north-south motion of the position of sunrise shows a maximum northern point on the Summer Solstice, and a maximum southern point on the Winter Solstice.
On the larger of the spheres we can strap on an additional loop, inclined at 5° to the ecliptic, to represent the cycle of the Moon. The Moon has a long term motion west to east of 13° per day, completing a circle relative to the celestial sphere in 27.3 days (sidereal month) and taking 29.5 days to catch up with the Sun (synodic month).
Setting it up:
The large Armillary Sphere (1m diameter) takes center stage on the floor; the smaller version (diameter 35cm) is a bench top piece. 1
Comments:
The motions of the planets cannot be explained using the celestial sphere because of the observed retrograde motion.
figure 1. The Celestial Sphere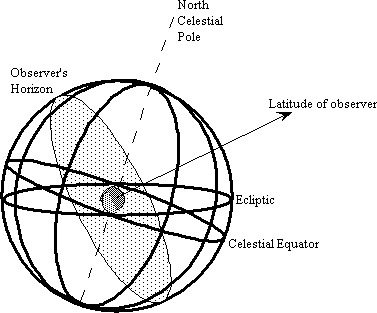
1 We're not sure of the origins of our spheres, but Central Scientific makes a couple of celestial globes, although they are more suited to classroom scales than lecture halls.