What it shows:
Using conservation of energy, calculate the height from which Barney must jump so that his head just barely kisses the floor at the bottom of his bungee cord jump. Then verify by experiment. Oops ... hate when that happens! It turns out that it's not so simple and there are important details that must be taken into account.
How it works:
Barney (the friendly pink dinosaur) is "sandbagged" (with a 5 kg weight, duct-taped around his waist) and suspended from the sky-hook by a 3.1 meter-long (unstretched) spring. The spring constant has been measured to be 32.7 N/m. The set-up is illustrated as follows:
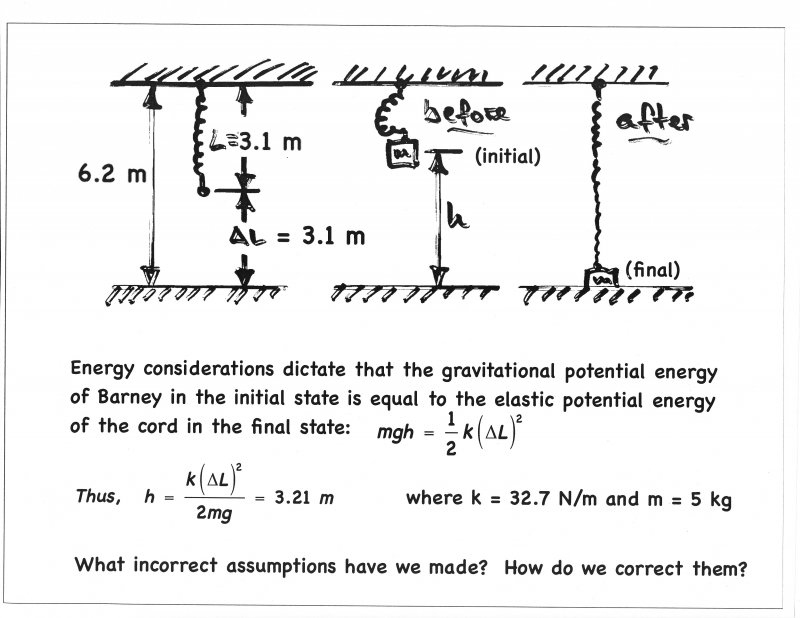
First, we have modeled Barney as a point mass, which he is not. The distance from his center-of-mass to the top of his head is approximately 25 cm, so we must correct ΔL to be 3.10 m - 0.25 m = 2.85 m.
Secondly, the elastic potential energy at the bottom needs to take into account the force required to start stretching the spring, as is deduced from actual data of force vs spring extension:
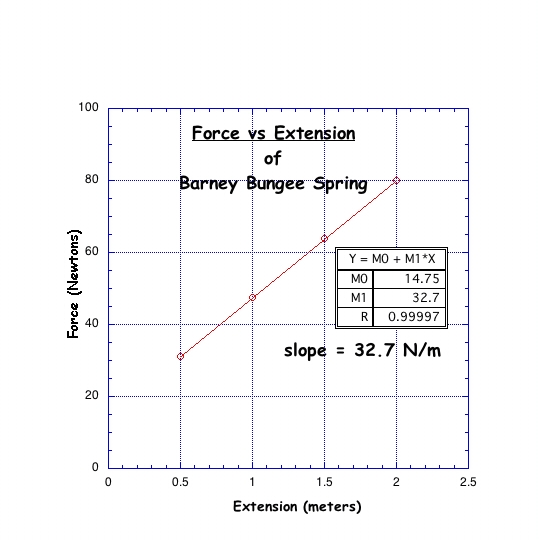
The Hooke's Law behavior of the spring is nice and linear, but extrapolating to the y-axis tells us that 14.75 N is required to just start stretching the spring. That force is present all the time in addition to the force required to stretch it further. Thus the total work done in stretching the spring is given by the triangular area under the force vs extension graph plus the rectangular area under the triangle: mgh = (½)k(ΔL)2 + (14.75 N)(ΔL). This yields a theoretical value for h = 3.56 m, which can be experimentally verified to be pretty close to what works.
Setting it up:
The bungee spring is secured to the ceiling Sky-Hook by means of a dedicated rig. Obviously the Hi-Jacker lift must be left in the lecture hall to perform the experiment. Supply a long tape-measure. Assume that Barney's weight is neglible compared to the 5 kg weight, but a scale may be used to make that convincing.
Comments:
The demonstration is a memorable way to make the point: keep it simple, but not so simple that it's wrong!