Electrically driven machine to represent retrograde planetary motion according to Aristotle's theory of concentric spheres.
What it shows:
This is the realization of a proposed solution to retrograde motion put forward by Eudoxus (427 - 347 B.C.). Here a combination of three uniform circular motions produces retrograde motion.
How it works:
The hippopede machine consists of three concentric rings, with a point on the innermost representing the position of the planet. The assembly in figure 1 is held vertically in a 1.20m square Dexion™ metal frame. The outer ring is made of 3cm wide 3mm steel; the inner rings of 3cm wide 1mm aluminum.
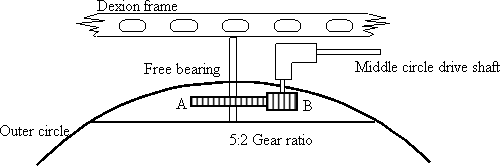
The outer ring is driven about its vertical axis by a 12V AC motor. The outer ring rotates freely about its upper spindle that has gear wheel A (figure 2) stationary and gear wheel B turning with the outer ring. Gear wheel B is linked through two right angle drives and two universal joints (with the connecting rod supported by bearing guides attached to the outer ring) to the middle ring which is driven about its horizontal axis. The inner ring is free to swing as the middle ring turns. It is weighted to remain horizontal by a semicircular bow of aluminum of equal radius to itself. As the apparatus moves, the spot on the inner ring describes a circular horizontal orbit with two retrograde steps every revolution.
table 1. Hippopede parameters
| Ring | Diameter (cm) | Rotation Speed (rpm) |
| Outer | 95 | 6.5 |
| Middle | 78 | 20 |
| Inner | 62 | 7 |
figure 1. The three circles of the Eudoxus Hippopede Machine
Comments:
Hippopede means horse-foot or horse-path. Horse training paths were typically laid out in a figure 8, which is the kind of retrograde motion suggested by this model. This machine, constructed by Bruce Collier, is designed to demonstrate the retrograde loops of the planet Mercury. Its only fault is that the inner ring tends to oscillate whereas it should always rotate in a fixed plane. Eudoxus, Plato's pupil, figured that you only needed 26 simultaneous uniform motions to account for the motions of all seven celestial bodies.
Professor Craig Sean McConnell has some excellent simulations on his website: http://faculty.fullerton.edu/cmcconnell/Planets.html
figure 2. Detail of the outer to middle circle gearing system