What it shows:
Hero's Principle states that light undergoing a reflection from a plane surface will follow the path of least distance. Here is a mechanical analog showing that when the angle of incidence equals the angle of reflection, the path length is minimized.
How it works:
The light path is represented by a 2m length of nylon rope that runs from a fixed end, 'reflects' around a pulley, back up to a second pulley (figure 1). The surplus rope is held taught by a 1kg mass. The pulleys, 6cm in diameter are free to move along the top and bottom rails of the frame on 1/2" ball bushing bearings. 1 The lower pulley represents the reflecting point, and it can be seen from the length of surplus rope, that any large displacement from an equal angle of incidence and reflection increases the path length. This experiment can also demonstrate the principle of stationarity; small displacements from the minimal path causes no noticeable change in the length of the surplus rope. This point of reflection is called a stationary point.
figure 1. Hero's Shortest Path frame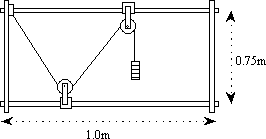
figure 2. Detail of bearing housing and pulley mount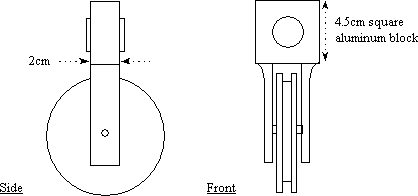
Setting it up:
The frame is constructed using lab clamps and bars, and clamps vertically to the front of a bench. Figure 2 shows the pre-assembled bearing and pulley module.

Comments:
Historically important contribution to the theory of light, presented by Hero of Alexandria 100 A.D. Following on, Damianus in 200 A.D. proposed that Hero's principle of least distance is equivalent to a principle of least time. Much later (1657) Pierre Fermat espoused the idea that light takes the path of least time. For light to choose to minimize both suggests a finite propagation velocity.
1 Barden Bearings, from Bearings Inc. 3600Euclid Ave., Cleveland Ohio 44115.