Standing sound waves in a glass pipe are made evident by the fountains of kerosene inside the pipe.

What it shows:

The air inside a very large glass pipe (partially filled with a fluid) is acoustically excited into a standing wave. Once resonating, the locations of the velocity antinodes inside the pipe are dramatically made evident by the vigorous agitation of the fluid, resulting in fabulous foaming frothing fountains of fluid. The velocity of sound can also be determined by noting the resonance frequency and measuring the distance between antinodes.

How it works:

The modes of vibration (resonances) of a one-end-open pipe are such that, at the closed end, the air motion is minimum (but the pressure is maximum) and the displacement of the air is greatest at the open end (with a corresponding minimum pressure variation). ¹ These boundary conditions are satisfied by odd multiples of 1/4 wavelengths and the resulting modes include odd-numbered harmonics only.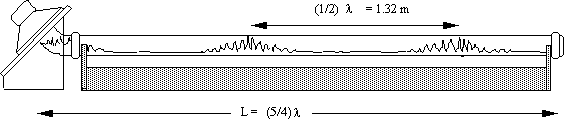



The horizontally oriented glass pipe ² is 10 ft (3.05 m) long and has an inside diameter of 4" (10 cm). One end is sealed off with a glass end-cap and the other end is terminated by a short 45° glass elbow and left open. Kerosene ³ partially fills the tube to a depth of 2 to 3 cm. A special light box ⁴ supports the pipe at the ends and illuminates it from below. A large loudspeaker, positioned over the open elbow, is closely coupled to it. ⁵ The elbow plus the speaker makes the total acoustic length equal to 3.30 m. A function (sine wave) generator ⁶ and power amplifier ⁷ drive the transducer.

Like the wind over the ocean, the intense displacement antinodes agitate the fluid into fountain-like waves that can be seen even from the back row of our largest lecture hall. The fundamental mode (L = 1/4 wavelength) occurs around 26 Hz and is so strong that it tends to splash kerosene into the speaker. The second harmonic (3/4 wavelength in tube) is just under 80 Hz; all the harmonics are separated by about 50 Hz. The illustration above depicts the third mode of vibration (frequency = 129 Hz). Once you get into the 200 Hz range and above, the sound becomes obnoxiously loud.

To measure the speed of sound, one simply measures the distance between two maxima and set that equal to half the wavelength. The easiest way to do this is to step back and visually judge where the maxima are and put tape marks in those locations. Then measure the distance between tape marks. For example, for the mode shown in the illustration, the distance turned out to be 1.32 m. Thus the wavelength is 2.64 m and (with a frequency of 129 Hz) the speed of sound = 341 m/sec. This is very close to the speed of sound in air (which is 343 m/sec at 20°C). The kerosene vapor, mixed with the air, undoubtedly depresses the speed slightly (the speed is inversely proportional to the square root of the molecular weight of the gas).

Closer inspection of the fluid fountains shows a much higher frequency periodicity superimposed upon the broad antinodes. The fluid fountains are regularly spaced sheets of fountains with a spacing of the order of two to four centimeters and could be due to the glass pipe itself vibrating. ⁸ However, the fact that the kerosene is perfectly quiescent at the velocity nodes, without any hint of high frequency perturbations, raises some doubts about glass pipe resonances. Another possibility is that these perturbations may be some kind of surface tension waves. Just before the surface breaks into the fountain effect, the surface becomes ripply in a most uniform manner - the ripples being regularly spaced about a millimeter apart. At the same time the overall level of the kerosene rises about 1/2 cm in this area and simultaneously falls by a similar amount at the velocity nodes (high pressure).

Setting it up:

Being quite long, the entire apparatus straddles two lecture carts and takes up a good bit of floor space. The kerosene is stored in the pipe (which is capped off at the elbow when not in use), eliminating the need to fill and drain this unwieldy piece of plumbing. The only prep work required is hooking up the electronics to the loudspeaker.

Comments:

The longitudinal motion of the vibrating air in a pipe is a little harder to visualize than the transverse vibrations of a string. This demonstration makes the invisible visible, or at least easier to conceptualize. It's very dramatic and visually appealing. We would like to give credit to Ned Kahn (artist-in-residence at the Exploratorium, San Francisco) who originally conceived and developed this demonstration in 1984. He was inspired by the Kundt's tube demonstration of standing waves in pipes (performed with cork dust or lycopodium powder). This demonstration replaces our old Hot Wire Standing Wave Tube, as it is much easier to see and less annoying to hear! We do not understand the exact mechanisms involved in creation of the fluid fountains. It is subtle and nonlinear effect as there seems to be a high threshold of power required to start the fountain effect. Also, there must be some kind of positive feedback in the fluid dynamics because intuitively one would think that the fountains would damp out, or at least impede, the motion of the air at the velocity antinodes. This does not seem to be at all the case. In fact, once the power threshold has been reached and the fountain effect starts, very little extra power is required to make the fountains larger.

1 In reality, the pressure variations do not drop to zero right at the open end of the pipe, but rather a small distance beyond. For a cylindrical pipe of radius r, the additional length is 0.61r. In this case, however, the speaker is closely coupled to the end of the pipe so that this end correction does not apply. Rather, the acoustic length of the pipe is the distance between the speaker cone and the closed end = 3.30 m.
2 A leftover sewer pipe from the Science Center.
3 Kerosene is the fluid of choice because of its relatively low surface tension and because it nicely wets the glass inside the tube, which makes for good visibility. Water will work, but much more excitation power is required and, once the fountains start, it's like trying to look through a windshield without wipers in a heavy downpour. About one gallon fills the tube to a good depth.
4 Two 4-foot fluorescent lights are permanent fixtures inside the box.
5 The speaker is an ALTEC model 803B 16" woofer, made by Lansing Corp. It's mounted on a baffle (at a 45° angle) which touches the glass elbow. A 4.5" (11.4 cm) diameter hole in the baffle acts like a port that couples the transducer to the pipe.
6 IEC model F34 function generator
7 Hafler model DH-200 audio amplifier
8 The speed of sound in Pyrex is 5640 m/sec (longitudinal) and 3280 m/sec (transverse). If these high frequency perturbations are due to longitudinal resonances in the glass, their frequencies are in the 70 kHz to 140 kHz range, i.e. ultrasonic. A spectral analysis of the sound emanating from the wave tube showed no spurious peaks up to 20 kHz, which suggests that these are indeed ultrasonic vibrations. Even finer periodic structure can be observed in the thin film of kerosene coating the inside of the glass - longitudinal striations with a periodicity of about 0.5 cm. If these too are ultrasonic resonances in the glass, they are of the order of 500-600 kHz! It would be nice to corroborate these speculations with an ultrasonic spectral analysis.