A physical pendulum with two adjustable knife edges for an accurate determination of "g".
What It Shows
An important application of the pendulum is the determination of the value of the acceleration due to gravity. By adding a second knife-edge pivot and two adjustable masses to the physical pendulum described in the Physical Pendulum demo, the value of g can be determined to 0.2% precision.
How It Works
Using a simple pendulum, the value of g can be determined by measuring the length L and the period T. The value of T can be obtained with considerable precision by simply timing a large number of swings, but comparable precision in the length of the pendulum is not so easy. For example, it's hard to estimate where exactly the center of the mass is.
To overcome this difficulty we can turn a physical pendulum into a so-called reversible (Kater's) 1 pendulum. Two knife-edge pivot points and two adjustable masses are positioned on the rod so that the period of swing is the same from either edge. The Kater's pendulum used in the instructional laboratories is diagramed below and its adjustments are described in the Setting It Up section.

The period for this arrangement can be proved 2 to be the same as that of a simple pendulum whose length L is the distance between the two knife edges.
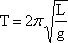
The distance between two knife edges can be measured with great precision (±0.05cm is easy). A digital wristwatch or large analog timer 3 is used to verify the period. By timing 100 or more swings, the period can be determined to an accuracy of fractions of a millisecond. Therefore, all other corrections and systematic errors aside, in principle it is possible to measure g to better than 0.2%.
Setting It Up
As in the Physical Pendulum demo, the pendulum knife-edge support is a U-shaped piece of aluminum that is clamped onto a standard lab bench rod. Use a 3/4" dia. iron rod, as rigidity is important. Rather than measure the distance between the two knife edges, it is easier to adjust them to a predetermined distance. A 3/4" square × 18" long 4 steel bar is supplied for this purpose. Adjustment of the positions of the knife edges and masses until the two periods are equal can be a lengthy iterative process, so don't leave it 'till lecture time. Find the positions before and mark them on the rod.
To determine the period, measure the total time of 100 swings of the pendulum. A typical value would be 2' 15.36" ± 0.10" (reaction time) giving T = 1.3536 sec, with an uncertainty of ±1 msec (timing multiple periods lessens the effect reaction time will have on the uncertainty of T). The formula then gives g = 9.811±0.015 m/s2. The value of g for Cambridge MA is 9.8038 m/s2.
Alternatively, one can set up a photogate and time the period of a swing with a laboratory frequency counter. This removes the reaction time uncertainty at the expense of adding a black-box complication to an otherwise simple experiment. However, one swing gives a value of g which is incredibly close to the accepted value.
Comments:
The demonstration has historical importance because this used to be the way to measure g before the advent of "falling rule" and "interferometry" methods. Indeed, the reversible pendulum measurement by Kühnen and Furtwängler 5 in 1906 was adopted as the standard for a world gravity network until 1968.
1 The reversible pendulum was first used to measure g by Captain Henry Kater: H. Kater, Philos Trans Roy Soc London 108, 33 (1818).
2 B. Crummett, The Physics Teacher 28, 291 (1990).
3 Sargent-Welch Scientific model 812
4 It's length was measured by the machine shop that made it and has the value 17.9265" stamped on its side. We don't put any weight on the last significant figure and this translates to 45.533 cm.
5 F. Kühnen and P. Furtwängler, Veroff Press Geodat Inst 27, 397 (1906). Their value was stated to have and uncertainty of ±0.003 cm/s2.