What it shows:
A changing magnetic flux induces a current in a metal ring; the magnetic field due to this current opposes the primary field, repelling the ring and flinging it into the air. That's the simple "hand waving" explanation for the beginner student—a more accurate explanation follows.
How it really works:
The jumping ring is a vivid and popular demonstration of electromagnetic induction and is used to illustrate Faraday's and Lenz's laws. A conducting ring, placed over the ferromagnetic core of a solenoid, may levitate or jump off when the solenoid is energized with sufficient 60-Hz alternating current. The changing magnetic flux induces an emf in the metal ring, producing a large current in the ring. The Lorentz force between the magnetic field and the induced current propels the ring.
The axial magnetic field of the iron core is responsible for inducing the current in the ring. The radial magnetic field provides the Lorentz force. Thus, the magnetic field must diverge out of the iron core since both axial and radial components are necessary for the effect. While this explanation is quite correct for an increasing magnetic field (as in the first 1/4 cycle), it is not the full story. Invoke the explanation for the case of alternating current and you will deduce that the net force (time-averaged over a complete cycle) is zero. There is one more subtle but very important feature that explains the effect in an AC magnetic field. See the Attractive and Repulsive Phases demonstration in-depth write-up for a graphical analysis of this.
The important feature missing from the explanation is the fact that the ring has an inductance. While this inductance is very small (0.043 μH)1, so is the DC resistance (61 μΩ)2. The total impedance of the ring is 63 μΩ, and there is a 15 degree phase angle between the induced emf and current in the ring. This phase angle is responsible for a non-zero time-averaged force. Decreasing the DC resistance (by cooling the Al ring in LN2) will not only increase the current in the ring, but will also increase the phase angle so that the Lorentz force on the ring is considerably greater (the ring hits the ceiling). If you increase the DC resistance (by using a stainless steel ring, for example), the phase angle is so small that no force can be detected on the ring.
It's also fun (and instructive) to hold one ring above (and close to) another hovering ring. The induced parallel currents in the two rings result in an attractive force between them, and the lower ring rises to touch the upper ring!
Much less obvious is why a stack of five narrow rings will hover higher than one single ring whose width is the same as the stack of five. An excellent and thorough analysis is given by P.J.H. Tjossem and V. Cornejo, "Measurements and mechanisms of Thomson's jumping ring," AJP 68(3), 238-244 (2000). See also P.J.H. Tjossem and E.C. Brost, "Optimizing Thomson's jumping ring," AJP 79(4), 353-358 (2011).
 |
 |
Apparatus details:
The solenoid sits vertically with the iron core—a 60cm long cluster of 1mm iron rods—resting inside it and protruding 42cm. The solenoid is a 400 turn coil with an air core inductance of 4.7mH, wound with 14 AWG wire insulated for 110V. The coil is connected to 110V AC.
Several rings are available. The "standard" ring is aluminum, 2 cm wide, 3.6 mm wall thickness, and 4.2 cm inner diameter to fit loosely over the core. Place the ring on top of the solenoid and turn on the power; the ring will shoot off the end of the core to a height of about 2m. Alternatively, turn on the power and place the ring over the core, and it will hover about half way up. A second aluminum ring is identical save for a split, which prevents a circuital current being set up so no field can be generated; the ring just sits there. Also available is a 50 turn (20AWG) wire loop connected to an 18V bulb. The induced EMF lights the bulb when the ring is lowered over the iron core; its brightness will increase dramatically as you move the ring down (see Comments).
figure 1. The Ring Flinger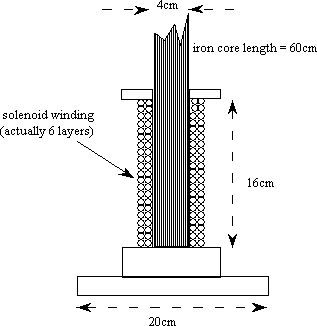
Setting it up:
The flinger sits on the lecture bench. Make sure the iron core is in place before turning on the supply; the low inductance will blow a fuse.
Comments:
For a much more spectacular fling, dip the ring into liquid nitrogen. This is explained in the Jumping Ring demo. Take care when using the coil and bulb, as it can easily burn out if dropped to the base of the rod, due to the very large flux down there. Apparently the jumping ring was first demonstrated by Elihu Thomson in May 1887 to the American Institute of Electrical Engineers in New York to help promote the supremacy of his ac dynamos over Edison's dc system.3
1 The inductance was calculated using the general equation on page 105, Chapt 13 of Frederick Grover, Inductance Calculations, (D Van Nostrand, 1946). The result agrees with another formula on page 95 for coils of square cross section.
2 The resistance was calculated for 6063 aluminum alloy, which has a resistivity = 3.32x10-6Ω-cm.
3 Noel Barry and Richard Casey, "Elihu Thomson's Jumping Ring in a Levitated Closed-Loop Control Experiment," IEEE Transactions on Education 42:1 (February 1999): 72-80.