What it shows:
An object rolling down a hill acquires both translational and rotational kinetic energy. One must take the rotational kinetic energy into account when calculating the object's velocity at the bottom of the hill
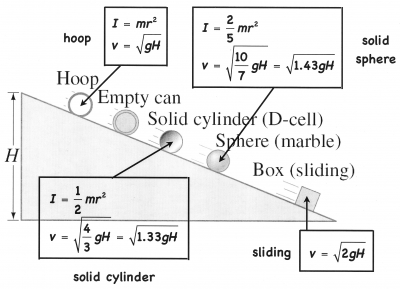
The illustration depicts the relative velocities of some common objects. Less common objects, which have been deviously altered, are also available.
How it works:
The inclined plane is 2½ meters long and is adjustable up to 20˚ w.r.t. the horizontal. It is wide enough (0.4 m) to race objects side-by-side down the hill. Since the velocities do not depend on the size or mass of the object, it's recommended that you first race similar objects: a bowling ball and billiard ball race ends in a tie, for example. You can also choose from a large selection of different size solid cylinders, hoops, etc. Having made the point, proceed to race objects with different rotational inertia. There are many possibilities for concept questions such as:
 |
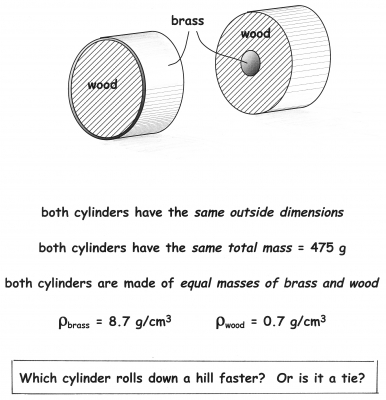 |
There are also wooden disks with off-center brass plugs (hidden from view) for irregular rolling. Other possibilities include unmarked tin cans filled with liquid, solid, sand (moving solid), or empty. Finally, you can race two plastic jars filled with water — the water in one jar has soap added to it while the other one does not. Which one is faster?
Setting it up:
The inclined plane occupies a good part of the lecture hall floor. Use a modest angle of incline (around 10 degrees or so) to keep the velocities on the lower side. That will make the races between objects more pronounced.
Comments:
This demo is a standard "must do."