Curved space segment for open universe geometry.
What it shows:
Whether the Universe continues to expand forever or will collapse back in upon itself depends upon the amount of matter it contains. For a density parameter Ω less than unity the Universe will not have enough mass to collapse and will be in a state of perpetual expansion. In general relativity, the curvature of space is dependent upon the density of the Universe, and for Ω<1 the curvature is negative or hyperbolic. It can be represented two dimensionally (see Comments) by a saddle shaped surface.
How it works:
The saddle shape is a plaster of Paris surface laid on a wooden frame of ribs cut to the contour of the shape. Ours has a 50 × 50cm base. The side walls are painted black and the surface itself white so it can be drawn on with chalk. You can use the surface to show examples of the non-Euclidean geometry of curved space. A circle will have a circumference less than 2πr and an area less than πr2. A triangle's angles will add to less than 180°, and two parallel lines will diverge.
figure 1a. Saddle Shape Surface figure 1b. Saddle Frame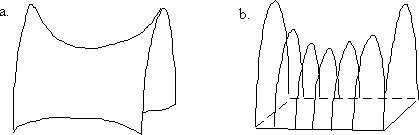
Setting it up:
Use colored chalk to draw your shapes on the surface. By mounting the saddle on a turntable, you can give your audience different perspectives.
Comments:
The saddle model is an imperfect analogy for an open universe because it possesses a center. The best representation is an infinite surface called a pseudosphere which is impossible to represent in three dimensional space. Our engineers are working on it...
For an artistic visualization, the painting Circle Limit IV by M. C. Escher is in fact the projection of a pseudosphere onto a plane. For a representation of the saddle shape using bubbles, see the Minimal Surfaces demo.