Optical technique that allows us to see small changes in the refractivity of air and other transparent media.
What it Shows
Refraction due to inhomogeneity in air is made visible by our single-mirror schlieren optics setup. The refraction can be caused by changes in the density, temperature, or pressure of the air immediately in front of the concave mirror. With a video camera and monitor, we can see warm convection currents rising from a candle flame or, alternatively, cold air sinking from a glass of ice water. The jet of warm air from an ordinary hair dryer is made dramatically visible.
The flow of gases other than air can also be visualized with this technique. For example, sulfur hexafluoride gas is six times more dense than air, and so can be visibly poured from a bottle into a glass as if it were a liquid.
This video of our setup shows the pressure antinodes of an ultrasonic standing wave as bright bands:
One can also demonstrate the diffraction of light around objects. By turning down most of the lights so that there is very little ambient illumination, an object placed in front of the mirror is seen as dark (not surprisingly), yet surrounded by a thin, bright outline of light. This light, whose origin is the point light source, is being diffracted around the edges of the object and into the camera.
How It Works
A long focal-length mirror is used to focus a point source of light onto a thin wire (or razor blade edge), which acts as a light block. Positioned directly behind the light block is a camera, which is looking at objects immediately in front of the mirror in the “test area.” If there is a change in the refractive index of the air in the test area, the image of the point light source will be deflected slightly. If it is deflected past the edge of the light block, the additional light that enters the camera will appear as streaks of light originating from the area where there was a change in the index of refraction; this is the so-called schlieren effect.
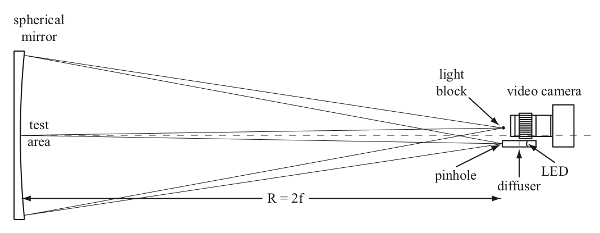
The brightness of the schlieren effect is proportional to the magnitude of the change in refraction—the greater the change in refraction, the greater the deflection of the point light image resulting in more light passing over the edge of the light block. Fundamentally, it is changes in the density that are responsible for changes in the refractivity (n − 1), where n is the index of refraction. For air and other gases, there is a simple linear relationship between the refractive index and the gas density, ρ, given by
n − 1 = kρ
where k is known as the Gladstone-Dale coefficient and is nearly constant over most of the visible spectrum. Its value for air is approximately 2.3×10-4 m3/kg. The expression for the angular deflection δ of the point light image by a density gradient perpendicular to the optical axis, say dρ/dx, is given by
δ = kL dρ/dx
where L is the span of the disturbance in the direction of the optical axis. Since density is proportional to pressure and inversely proportional to temperature, any changes in these attributes are likewise made visible.
Because large changes in the density of a gas corresponds to only a small change in the index of refraction, the schlieren system has to be sensitive enough to detect deflections of only a few arcseconds of angle. The optical leverage needed to make these small deflections apparent requires a spherical mirror with a focal length of a few hundred centimeters, and shaped to a high tolerance. To provide enough contrast between the refracted light and the dark background, the diameter of the point light image needs to be a fraction of a millimeter, while the light source should be able to give several hundred lumens of flux.
For further research, Schlieren and Shadowgraph Techniques—Visualizing Phenomena in Transparent Media (Springer-Verlag, Berlin, Heidelberg, New York, 2001) by G. S. Settles is an excellent book from one of the leading authorities on the subject. Provided are technical details as well as historical background.
Setting It Up
The setup—including the spherical mirror, light source, light block, and video camera—requires careful alignment in a space that is at least 7 meters long and 2 meters wide. The effect can only be seen through the video camera, so either a large monitor or a projection system is needed.
Equipment
(a) The point light source that we usually use is a small battery-powered white LED flashlight positioned behind a 400 micron Melles Griot pinhole with Vellum inserted between the two for uniform illumination. These are all mounted together in a housing that is attached to an optics rail.
(b) The light block we most often use is a razor blade mounted on an x-y adjustable optics post, which is mounted to the optics rail and oriented so that the blade can be moved vertically as well as longitudinally in the direction of the mirror. Alternately, a size 7 piano wire (0.018 inch diameter) mounted in a lens holder can also be used, but keep in mind this works best with the 500 micron pinhole instead of the 400 micron one.
(c) The spherical mirror is a 12.5" (31.8 cm) diameter, 123" (312 cm) focal length, f/10, protected aluminum mirror from Edmund Scientific (the mirror mount was donated to us from the late Costas Papaliolios). When space is limited, we also have an 18” diameter, 2 meter focal length, f/4.3 mirror that we salvaged from a spectrometer.
(d) The video camera we currently use is a Blackmagic Pocket Cinema Camera, which we have adapted to fit a Canon TV-16 25-100 mm f/1.8 Zoom Lens. An Asahi Takumar 300 mm f/6.3 lens with a Zhongyi Lens Turbo 2 speed booster can also be used for tighter shots. The lens is attached to the optics rail via a specially made mount. The light block should be positioned close enough to the lens so that it is completely out of focus.
(e) To speed up the alignment procedure, an adapter has been made to mount a HeNe laser onto the C-mount thread of the zoom lens (the video camera of course needs to be removed).
(f) The most convenient support for the telescope mirror is the sturdy angle-iron stand normally used for the Cavendish experiment. The Spindler & Hoyer optics rail (on the tripod mount) is also nice and sturdy and fully adjustable.
Alignment
(1) Level the optics rail on which the point light source, razor blade, and zoom lens/laser is mounted. Position the telescope mirror a distance of two focal lengths from the razor blade, lock the mirror stand into place with the leveling screws, and adjust the height of the optics rail so that the laser beam hits the telescope mirror in the middle.
(2) Rotate the mirror/mirror holder to direct the laser beam back towards the pinhole. Fine-adjust the mirror (using the horizontal and vertical adjustment screws) to precisely hit the pinhole with the beam. Remove the laser from the lens and mount the video camera.
(3) Stop the lens way down (typically f/22). This produces a hexagonal vignetting pattern (from lens iris). Re-adjust the telescope mirror (with the fine adjustment screws) so that this hexagonal pattern is centered in the mirror (this part is crucial for best results!).
(4) Raise the light block and slide its mount back and forth on the optics rail to coarsely focus the point light source on the blade; fine tune the focusing with the longitudinal adjustment screw (on the razor blade mount). Lower the razor blade so that its edge just barely cuts off the point source image. Open up the lens to maximum aperture and fine tune razor edge height. Focus the lens on whatever object is held in front of the mirror.
Comments
The most dramatic effects are seen when the object that disturbs the optical path is right in front of the mirror. Take care not to touch the mirror! It is extremely sensitive when properly aligned; an occasional draft will look like a passing cloud. Heat from your hand rises up in wisps while air, chilled by a glass of ice water, sinks rapidly. A heated soldering iron looks like it's on fire. Sulfur hexafluoride gas appears to be a liquid pouring out of a container.
Although a bit of a bear to set up, the demonstration is very rewarding with stunningly beautiful geometric and physical optics effects.
