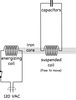
A 60 Hz AC magnetic flux from an iron core induces an emf in a suspended coil of wire. With appropriate capacitance added, the coil will be attracted to, repelled from, or not affected by the magnetic flux.
What it shows:
When the suspended coil is part of a complete circuit, the induced emf in the coil will drive a current through that circuit. As seen in the RLC Resonance Circuit demonstration, the phase between the current and the emf depends on the frequency; the current is in phase at resonance, leads the emf at frequencies below resonance, and lags the emf above resonance. Since the current interacts with the magnetic field, the net Lorentz force on the current (and therefore the coil) will depend on their phase relationship.

|

|
How it works:
In this experiment we keep the frequency fixed (60 Hz) but vary the resonance frequency of the RLC circuit by changing the capacitance. Thus, depending on the capacitance, 60 Hz may be (1) at, (2) above, or (3) below, the resonance frequency of the circuit.
(1) At resonance, the phasor representations of the inductive and capacitive reactances are equal in magnitude and 180˚ out of phase with each other. Thus the total impedance of the circuit is purely resistive and the current is in phase with the emf. The following graphic depicts the phase relationships between the various parameters, including the Lorentz force on the current in the coil. Since the Lorentz force is equal to the cross product of the current and magnetic field, the graph was generated by simply taking the product of the induced current graph and the magnetic flux graph. [Note that the magnetic field from the iron core actually diverges and the interaction responsible for pushing the coil longitudinally is with the radial component of the magnetic field through the coil; the longitudinal component generates the emf.]
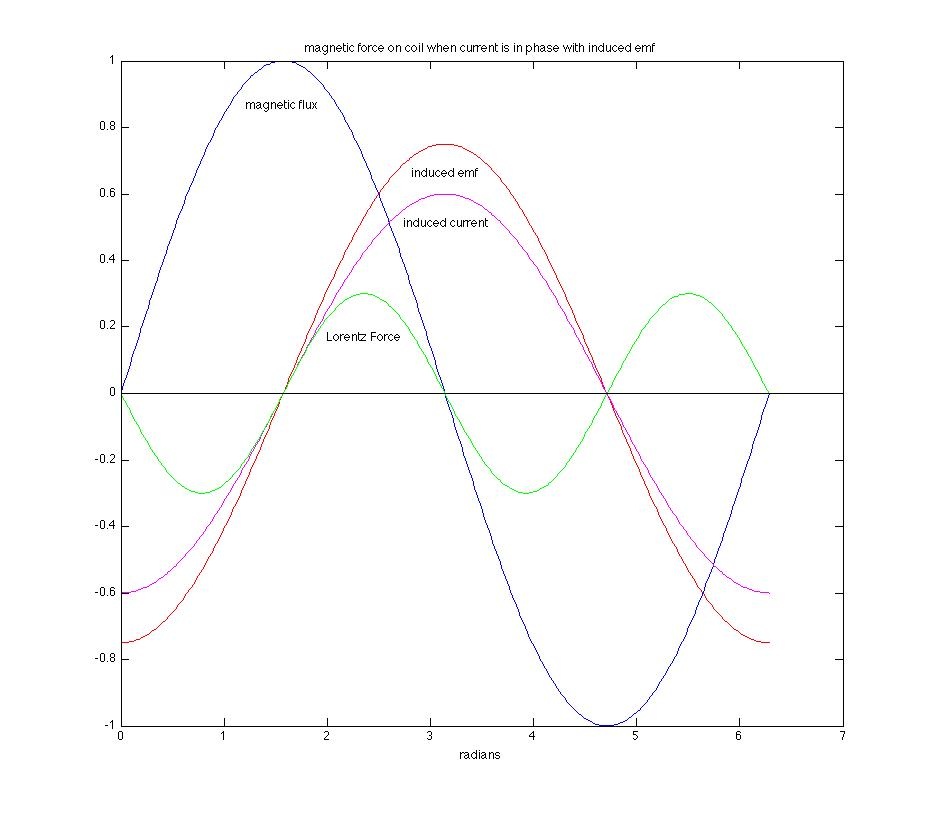
The vertical scale is arbitrary, but nevertheless, one can see that the net force on the coil is zero in one complete cycle of the magnetic flux—it is as much negative as it is positive. When an appropriate capacitor is connected across the coil to make the circuit's resonance frequency equal to 60 Hz, the current is in phase with the emf and the coil is neither attracted to nor repelled by the magnetic field. [As a side note, this is exactly the reason why simply invoking Lenz's Law is not enough to explain the action of the Ring Flinger demonstration.]
(2) If a larger capacitor is connected across the coil, the resonance frequency of the RLC circuit will decrease. Since the frequency of the induced emf remains fixed at 60 Hz, the current in the circuit will be driven above resonance. At frequencies above resonance, the inductive reactance becomes greater than the capacitive reactance and that leads to a phase shift between the current and the emf (as can be shown with a phasor diagram). In effect, the RLC circuit has become "more inductive" in nature and the current will lag the emf accordingly. The phase relationships between the various parameters are shown for the case when the current lags by 30˚.
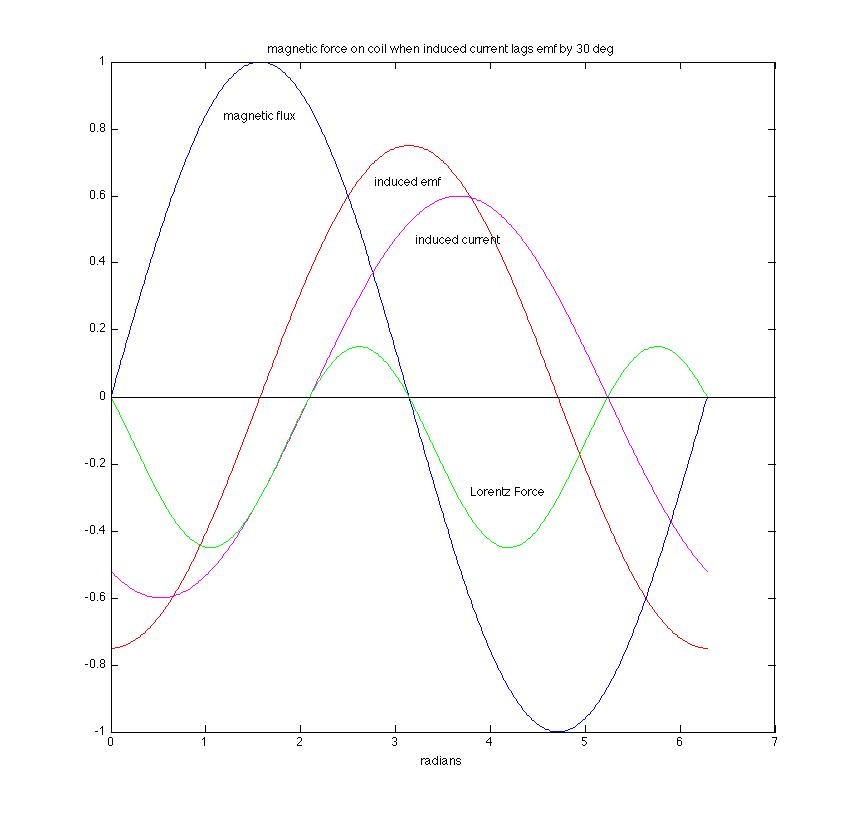
Now we see that there is a net negative Lorentz force over one cycle. This leads to a net repulsive force between the current-carrying coil and the magnetic field. The coil gets pushed away! If one imagines the frequency of the driving emf getting larger and larger with respect to the resonance frequency, the circuit behaves more and more "inductively" and the current lag increases accordingly. The limit is, of course, 90˚ (for a simple RL circuit in which the inductive reactance completely dominates any capacitive reactance) and that is shown in the next figure.
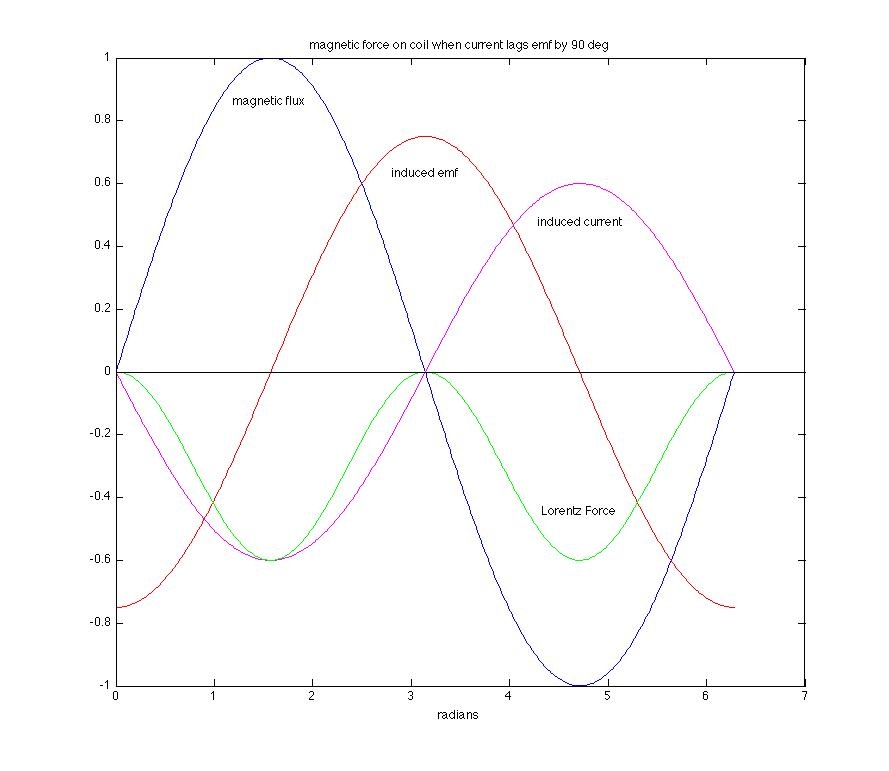
In this case the net Lorentz force is negative during the entire cycle and the coil will be repelled maximally.
(3) If a smaller capacitor is connected across the coil, the resonance frequency of the RLC circuit will increase. Again, the frequency of the induced emf remains fixed at 60 Hz, and thus the current in the circuit will be driven below the resonance. At frequencies below resonance, the capacitive reactance becomes greater than the inductive reactance and that leads to the opposite phase shift between the current and the emf. In effect, the RLC circuit has now become "more capacitive" in nature and the current will lead the emf. The phase relationships between the various parameters are shown for the case when the current is leading by 30˚.
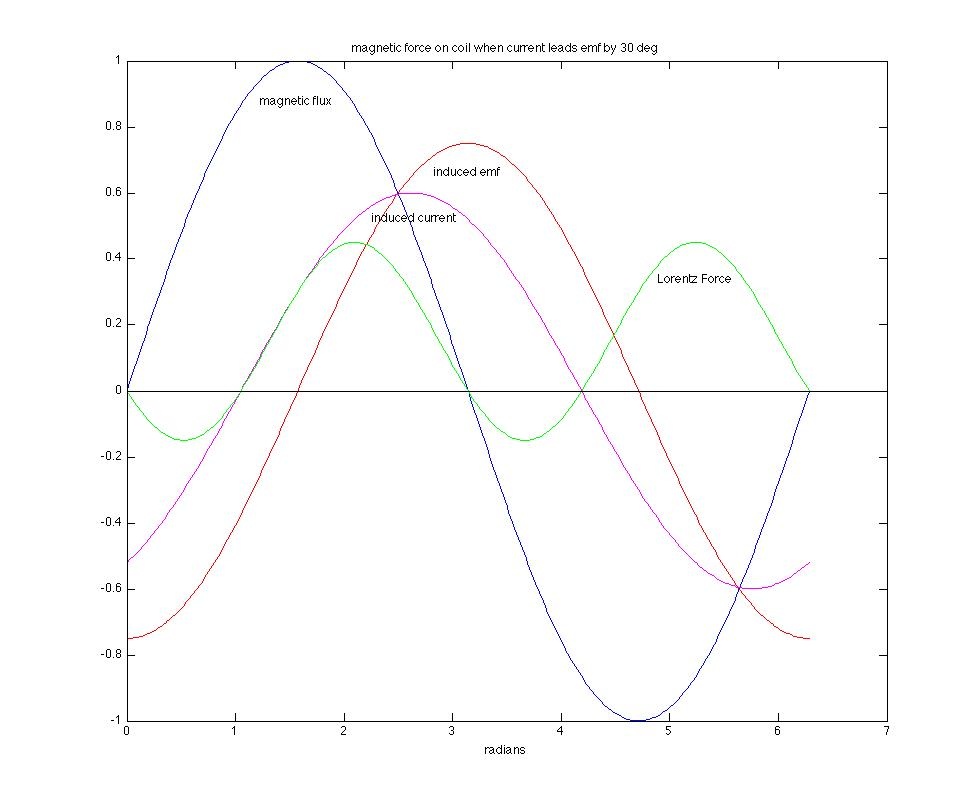
Now we see that there is a net positive Lorentz force over one cycle. This leads to a net attractive force between the current-carrying coil and the magnetic field. The coil gets pulled in! Again, if we imagine the frequency of the driving emf getting smaller and smaller with respect to the resonance frequency, the circuit behaves more and more "capacitively" and the current lead becomes larger. The limit is again 90˚ (for a simple RC circuit) and that is shown in the next figure.
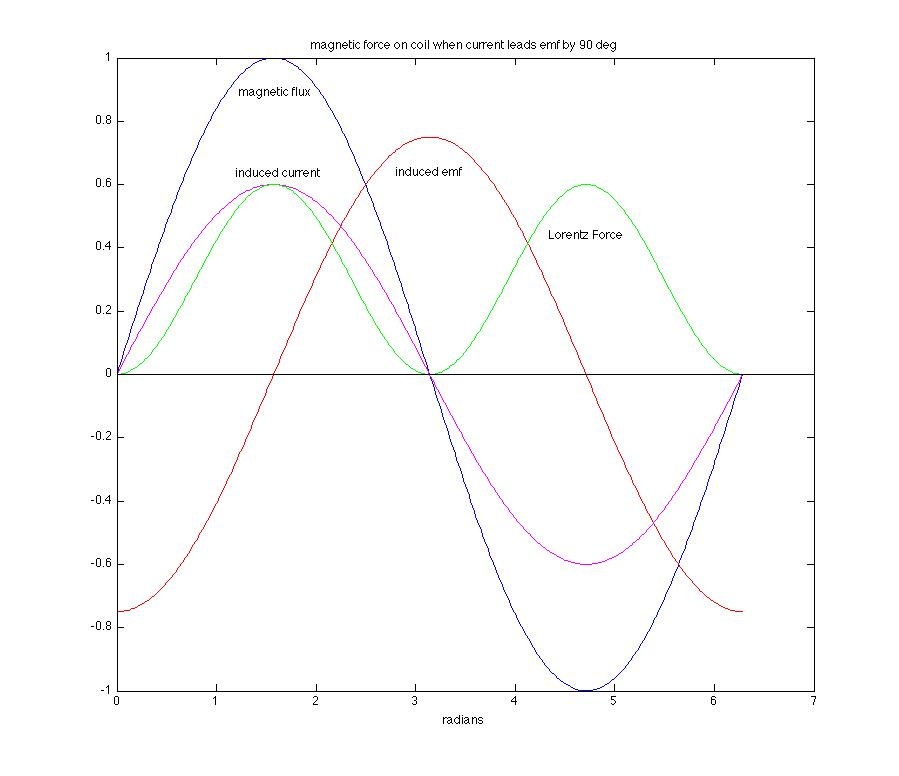
In this case the net Lorentz force is positive throughout the cycle and the coil will be attracted maximally.
Details:
The examples given above are meant to provide a graphic argument for the effect observed. And now for the actual details of the apparatus.
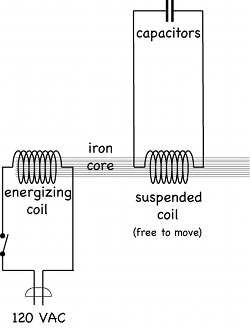
The coil measures 15 cm long and consists of 500 turns of #16 wire wound in 5 layers. The inside core diameter is 3.75 cm. DC resistance = 1.3 Ω and inductance = 4.5 mH (with air-filled core). When the iron core is inserted into the coil, inductance = 27.8 mH (measured at 60 Hz). The coil is suspended by the wires that connect it to the capacitors and is free to move.
A bank of 60 µF capacitors plus a 15 µF are wired in parallel in various combinations and connected to the coil via its suspension wires:
(a) When three 60 µF caps (total = 180 µF) are connected to the coil, it experiences a strong attraction. In this case Xc = 14.7 Ω, XL = 10.5 Ω, and the current lags by -73˚.
(b) When five 60 µF caps (total = 300 µF) are connected to the coil, it experiences a strong repulsion. In this case Xc = 8.8 Ω, XL = 10.5 Ω, and the current leads by +53˚. One can also eliminate the capacitors entirely and simply short out the coil with its connecting wires. In this case there is a very strong repulsion. We now have a simple RL circuit in which the current leads by 90˚ and, from the analysis above, one expects the strongest effect. (It's also instructive to completely disconnect the coil — with an open circuit, no current can flow and thus there's no Lorentz force, just like the split ring in the Jumping Ring demo.)
(c) When four 60 µF plus a 15 µF (total = 255 µF) caps are connected, there is no net attraction or repulsion. In this case Xc ≈ XL = 10.5 Ω, and the current is in phase with the emf. It should be noted that the coil does experience a small initial repulsive "kick" when the switch is thrown. This transient effect is to be expected, due to the first quarter cycle of flux change. If the coil is held in place when the switch is thrown, and then released, it remains hanging in its neutral position.
Comments:
The switch between attraction and repulsion of the coil can be quite mysterious and this demo goes a long way toward understanding the underlying physics. It certainly helps clear up the subtleties of the Ring Flinger demonstration.